工作中遇到了一些问题，经过请教同事，原来用向量来处理很简单，大脑挣扎的回忆了下才想起来多年前就还给老师了，惭愧惭愧……特意查了查以备后续查看.

场景

一条任意曲线，鼠标点击曲线上任意一点，然后鼠标可以任意方向移动，在移动的过程中需要实时更新当前点的位置.类似于下面这种情景:

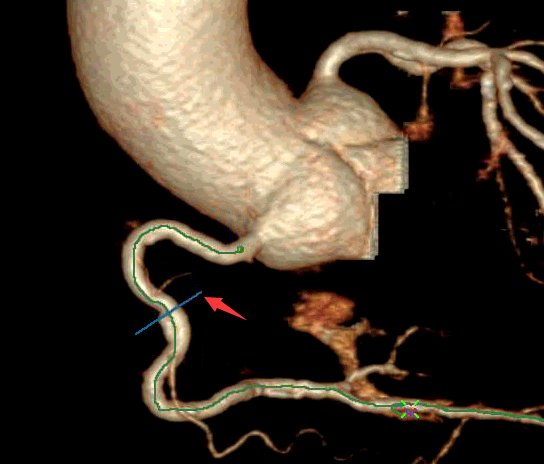
鼠标可以拖住曲线(血管)上剖切线沿着任意方向移动，移动过程中实时更新位置.

问题

• 如何确定当前鼠标是向上移动了还是向下移动了?
• 鼠标会沿任意方向移动，不一定在曲线上移动.

分析

问题的关键就在于如何确定鼠标是上移还是下移(或者左移/右移，因为曲线是任意方向的)，难点就在于确定鼠标方向

解决思路

思路其实很简单了，从鼠标点击的位置其前后位置的点，然后鼠标移动过程中也有一个点，利用这几个点可以构造三个向量，如下图所示. 我们知道如果两个向量相乘大于0，那么他们之间的夹角肯定小于90度，反之大于90度，由此可以知道当前鼠标位置是向下还是向上移动。

向量的夹角为[0~π],根据向量夹角公式可以得出，如果两个向量积大于0，那么其夹角比小于90度.

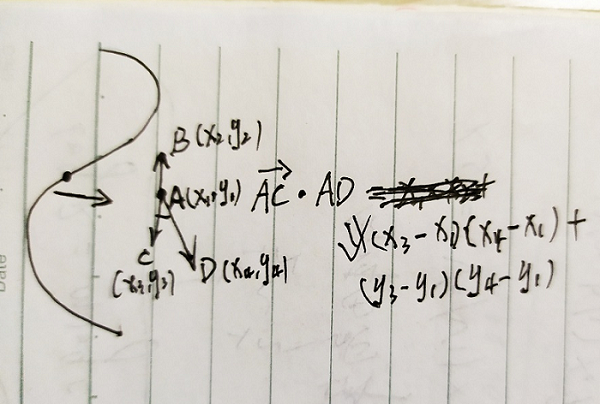
向量

现在轮到向量登场了，啥是向量?

在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量），数量（或标量）只有大小，没有方向。

平面内任意亮点向量坐标

任意向量坐标 = 终点坐标 - 起点坐标

向量夹角公式

根据向量点乘可知，鼠标起点前后点位置取一个即可，根据鼠标当前位置，构造2个向量，计算后可以知道当前的方向.

核心思想

int getMouseStatus(QPointF &ptCurrent)
{
    QPointF ptCenter;   /*! 鼠标位置起点*/
    QPointF ptBefore;   /*! 起点前一个点*/
    QPointF ptBehind;   /*! 起点后一个点*/

    QPointF ptBeforeTemp = ptBefore - ptCenter;
    QPointF ptBehindTemp = ptBehind - ptCenter;
    QPointF ptOffset = ptCurrent - ptCenter;

    /*!
     * 如果nValue = 0,则表示垂直;
        > 0 上移, < 0下移
    */
    int nValue = ptBeforeTemp.x() * ptOffset.x() + ptBeforeTemp.y()* ptOffset.y();

    return nValue;
}

这些年曾经学过的知识可能都还给老师了，但是老师常说的话却深深印在脑海里.活到老学到老，尤其在这个越发浮躁的世界，多读点书，多学习下，时光不会亏待自己的.

Ps:这几天比较火的[流浪大师]，因为口出不凡一下子火了，当下人都太浮躁了，维流量、金钱第一，都不愿意读书，这恰恰体现出读书的重要性，当社会上读书的人越来越少时，我们读书的价值就会更大。

作者:鹅卵石
时间: 2019年3月27日20:33:11
版本:V 0.0.1
邮箱:kevinlq@163.com
版权:本博客若无特别声明，均属于作者原创文章，欢迎大家转载分享。但是，
希望您注明来源，并留下原文地址，这是对作者最大的尊重，也是对知识的尊重。

如果您对本文有任何问题，可以在下方留言，或者Email我.

捐赠

如果觉得分享的内容不错，可以请作者喝杯咖啡.